Calculate the Answer to Part B Again Using the Ideal Gas Tables Rather Than Constant Specific Heat
Temperature and Heat
5 Heat Transfer, Specific Rut, and Calorimetry
Learning Objectives
By the stop of this section, you will be able to:
- Explicate phenomena involving heat as a course of energy transfer
- Solve issues involving rut transfer
We have seen in previous chapters that energy is one of the primal concepts of physics. Rut is a type of energy transfer that is caused by a temperature difference, and it can alter the temperature of an object. As we learned before in this chapter, heat transfer is the motility of energy from i place or material to some other equally a event of a difference in temperature. Heat transfer is primal to such everyday activities every bit home heating and cooking, as well equally many industrial processes. It too forms a basis for the topics in the residue of this chapter.
Nosotros also innovate the concept of internal energy, which can be increased or decreased by heat transfer. We discuss another style to change the internal energy of a system, namely doing piece of work on information technology. Thus, we are beginning the study of the human relationship of heat and work, which is the basis of engines and refrigerators and the central topic (and origin of the name) of thermodynamics.
Internal Free energy and Heat
A thermal arrangement has internal energy (besides called thermal free energy ), which is the sum of the mechanical energies of its molecules. A system'southward internal energy is proportional to its temperature. Every bit nosotros saw before in this chapter, if two objects at different temperatures are brought into contact with each other, energy is transferred from the hotter to the colder object until the bodies attain thermal equilibrium (that is, they are at the same temperature). No work is washed by either object because no forcefulness acts through a distance (every bit nosotros discussed in Work and Kinetic Energy). These observations reveal that heat is free energy transferred spontaneously due to a temperature difference. (Figure) shows an instance of estrus transfer.
(a) Here, the soft drink has a higher temperature than the ice, so they are non in thermal equilibrium. (b) When the soft drink and ice are allowed to interact, heat is transferred from the beverage to the ice due to the difference in temperatures until they attain the same temperature, ![]() , achieving equilibrium. In fact, since the soft potable and ice are both in contact with the surrounding air and the bench, the ultimate equilibrium temperature will be the same equally that of the surroundings.
, achieving equilibrium. In fact, since the soft potable and ice are both in contact with the surrounding air and the bench, the ultimate equilibrium temperature will be the same equally that of the surroundings.
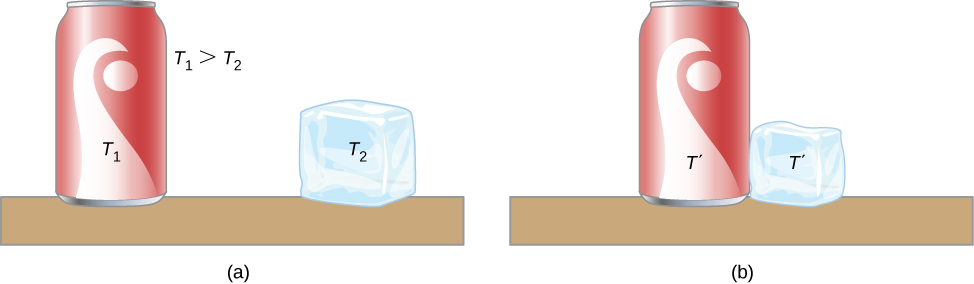
The meaning of "heat" in physics is unlike from its ordinary meaning. For example, in conversation, we may say "the estrus was unbearable," but in physics, we would say that the temperature was high. Rut is a form of energy flow, whereas temperature is not. Incidentally, humans are sensitive to heat catamenia rather than to temperature.
Since rut is a form of energy, its SI unit is the joule (J). Another common unit of energy oft used for heat is the calorie (cal), defined equally the energy needed to change the temperature of 1.00 thou of water past ![]() —specifically, between
—specifically, between ![]() and
and ![]() , since at that place is a slight temperature dependence. Also commonly used is the kilocalorie (kcal), which is the free energy needed to change the temperature of ane.00 kg of water by
, since at that place is a slight temperature dependence. Also commonly used is the kilocalorie (kcal), which is the free energy needed to change the temperature of ane.00 kg of water by ![]() . Since mass is almost often specified in kilograms, the kilocalorie is user-friendly. Confusingly, food calories (sometimes chosen "big calories," abbreviated Cal) are actually kilocalories, a fact not easily adamant from package labeling.
. Since mass is almost often specified in kilograms, the kilocalorie is user-friendly. Confusingly, food calories (sometimes chosen "big calories," abbreviated Cal) are actually kilocalories, a fact not easily adamant from package labeling.
Mechanical Equivalent of Heat
It is also possible to alter the temperature of a substance past doing work, which transfers energy into or out of a system. This realization helped found that heat is a form of energy. James Prescott Joule (1818–1889) performed many experiments to found the mechanical equivalent of heat—the work needed to produce the same effects as heat transfer. In the units used for these ii quantities, the value for this equivalence is
![]()
We consider this equation to represent the conversion between 2 units of energy. (Other numbers that y'all may see refer to calories defined for temperature ranges other than ![]() to
to ![]() .)
.)
(Effigy) shows i of Joule'due south well-nigh famous experimental setups for demonstrating that work and heat tin produce the same furnishings and measuring the mechanical equivalent of heat. It helped establish the principle of conservation of energy. Gravitational potential free energy (U) was converted into kinetic energy (Thou), then randomized by viscosity and turbulence into increased average kinetic energy of atoms and molecules in the system, producing a temperature increase. Joule's contributions to thermodynamics were and then significant that the SI unit of energy was named subsequently him.
Joule'due south experiment established the equivalence of heat and piece of work. As the masses descended, they acquired the paddles to do work, ![]() , on the h2o. The result was a temperature increase,
, on the h2o. The result was a temperature increase, ![]() , measured past the thermometer. Joule plant that
, measured past the thermometer. Joule plant that ![]() was proportional to W and thus determined the mechanical equivalent of heat.
was proportional to W and thus determined the mechanical equivalent of heat.
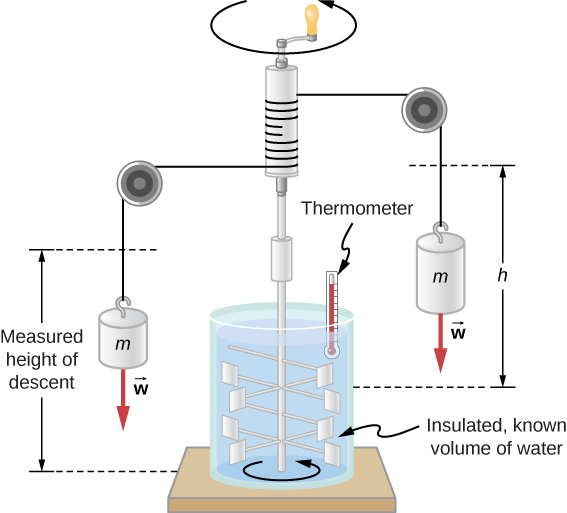
Increasing internal free energy by estrus transfer gives the same event as increasing information technology by doing work. Therefore, although a organization has a well-defined internal energy, we cannot say that it has a certain "heat content" or "work content." A well-divers quantity that depends only on the electric current state of the arrangement, rather than on the history of that arrangement, is known every bit a state variable . Temperature and internal energy are state variables. To sum up this paragraph, heat and work are not state variables.
Incidentally, increasing the internal energy of a system does non necessarily increase its temperature. Every bit we'll see in the next department, the temperature does not change when a substance changes from one stage to another. An example is the melting of water ice, which can exist accomplished by calculation heat or by doing frictional work, every bit when an ice cube is rubbed against a rough surface.
Temperature Change and Heat Capacity
We have noted that oestrus transfer often causes temperature alter. Experiments show that with no phase change and no piece of work done on or by the organisation, the transferred heat is typically direct proportional to the modify in temperature and to the mass of the system, to a skillful approximation. (Below we bear witness how to handle situations where the approximation is not valid.) The constant of proportionality depends on the substance and its phase, which may be gas, liquid, or solid. We omit give-and-take of the fourth phase, plasma, because although it is the most common phase in the universe, it is rare and brusque-lived on Earth.
We tin sympathise the experimental facts by noting that the transferred heat is the alter in the internal free energy, which is the total energy of the molecules. Under typical conditions, the total kinetic energy of the molecules ![]() is a abiding fraction of the internal energy (for reasons and with exceptions that we'll run across in the adjacent chapter). The average kinetic free energy of a molecule
is a abiding fraction of the internal energy (for reasons and with exceptions that we'll run across in the adjacent chapter). The average kinetic free energy of a molecule ![]() is proportional to the accented temperature. Therefore, the change in internal energy of a organisation is typically proportional to the change in temperature and to the number of molecules, N. Mathematically,
is proportional to the accented temperature. Therefore, the change in internal energy of a organisation is typically proportional to the change in temperature and to the number of molecules, N. Mathematically, ![]() The dependence on the substance results in big role from the unlike masses of atoms and molecules. We are considering its rut capacity in terms of its mass, but as we will see in the side by side affiliate, in some cases, oestrus capacities per molecule are similar for dissimilar substances. The dependence on substance and phase also results from differences in the potential energy associated with interactions between atoms and molecules.
The dependence on the substance results in big role from the unlike masses of atoms and molecules. We are considering its rut capacity in terms of its mass, but as we will see in the side by side affiliate, in some cases, oestrus capacities per molecule are similar for dissimilar substances. The dependence on substance and phase also results from differences in the potential energy associated with interactions between atoms and molecules.
Heat Transfer and Temperature Change
A applied approximation for the relationship between rut transfer and temperature change is:
![]()
where Q is the symbol for oestrus transfer ("quantity of rut"), yard is the mass of the substance, and ![]() is the change in temperature. The symbol c stands for the specific rut (also called "specific estrus capacity") and depends on the material and phase. The specific heat is numerically equal to the amount of heat necessary to change the temperature of
is the change in temperature. The symbol c stands for the specific rut (also called "specific estrus capacity") and depends on the material and phase. The specific heat is numerically equal to the amount of heat necessary to change the temperature of ![]() kg of mass by
kg of mass by ![]() . The SI unit for specific oestrus is
. The SI unit for specific oestrus is ![]() or
or ![]() . (Recall that the temperature modify
. (Recall that the temperature modify ![]() is the same in units of kelvin and degrees Celsius.)
is the same in units of kelvin and degrees Celsius.)
Values of specific heat must generally be measured, considering there is no simple way to calculate them precisely. (Figure) lists representative values of specific oestrus for various substances. We see from this table that the specific heat of h2o is five times that of glass and ten times that of iron, which means that it takes five times as much estrus to raise the temperature of water a given amount every bit for glass, and x times as much every bit for iron. In fact, water has one of the largest specific heats of whatever material, which is important for sustaining life on Globe.
The specific heats of gases depend on what is maintained constant during the heating—typically either the volume or the pressure. In the table, the offset specific heat value for each gas is measured at constant volume, and the 2d (in parentheses) is measured at constant pressure. We volition return to this topic in the chapter on the kinetic theory of gases.
| Substances | Specific Heat (c) | |
|---|---|---|
| Solids | | |
| Aluminum | 900 | 0.215 |
| Asbestos | 800 | 0.nineteen |
| Concrete, granite (average) | 840 | 0.xx |
| Copper | 387 | 0.0924 |
| Glass | 840 | 0.20 |
| Gilded | 129 | 0.0308 |
| Human body (average at | 3500 | 0.83 |
| Ice (average, | 2090 | 0.50 |
| Fe, steel | 452 | 0.108 |
| Lead | 128 | 0.0305 |
| Silver | 235 | 0.0562 |
| Wood | 1700 | 0.40 |
| Liquids | ||
| Benzene | 1740 | 0.415 |
| Ethanol | 2450 | 0.586 |
| Glycerin | 2410 | 0.576 |
| Mercury | 139 | 0.0333 |
| Water | 4186 | 1.000 |
| Gases [3] | ||
| Air (dry) | 721 (1015) | 0.172 (0.242) |
| Ammonia | 1670 (2190) | 0.399 (0.523) |
| Carbon dioxide | 638 (833) | 0.152 (0.199) |
| Nitrogen | 739 (1040) | 0.177 (0.248) |
| Oxygen | 651 (913) | 0.156 (0.218) |
| Steam | 1520 (2020) | 0.363 (0.482) |
In general, specific heat likewise depends on temperature. Thus, a precise definition of c for a substance must be given in terms of an minute change in temperature. To exercise this, nosotros notation that ![]() and replace
and replace ![]() with d:
with d:
![]()
Except for gases, the temperature and book dependence of the specific heat of most substances is weak at normal temperatures. Therefore, we will generally take specific heats to be abiding at the values given in the table.
Calculating the Required Heat A 0.500-kg aluminum pan on a stove and 0.250 L of h2o in it are heated from ![]() to
to ![]() . (a) How much heat is required? What percentage of the heat is used to enhance the temperature of (b) the pan and (c) the water?
. (a) How much heat is required? What percentage of the heat is used to enhance the temperature of (b) the pan and (c) the water?
Strategy We tin can assume that the pan and the water are always at the aforementioned temperature. When you put the pan on the stove, the temperature of the h2o and that of the pan are increased by the aforementioned amount. We use the equation for the heat transfer for the given temperature change and mass of water and aluminum. The specific heat values for water and aluminum are given in (Figure).
Solution
- Calculate the temperature difference:
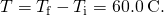
- Calculate the mass of water. Considering the density of water is
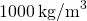 , one 50 of water has a mass of 1 kg, and the mass of 0.250 L of water is
, one 50 of water has a mass of 1 kg, and the mass of 0.250 L of water is 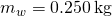 .
. - Summate the rut transferred to the h2o. Employ the specific oestrus of water in (Effigy):
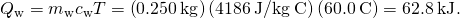
- Calculate the rut transferred to the aluminum. Use the specific heat for aluminum in (Figure):
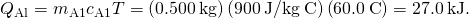
- Notice the total transferred estrus:
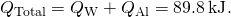
Significance In this case, the heat transferred to the container is a significant fraction of the full transferred heat. Although the mass of the pan is twice that of the h2o, the specific oestrus of h2o is over four times that of aluminum. Therefore, information technology takes a bit more than twice as much heat to attain the given temperature modify for the h2o as for the aluminum pan.
(Figure) illustrates a temperature rise caused past doing piece of work. (The result is the same every bit if the same corporeality of energy had been added with a blowtorch instead of mechanically.)
Calculating the Temperature Increment from the Work Done on a Substance Truck brakes used to control speed on a downhill run practice work, converting gravitational potential energy into increased internal energy (higher temperature) of the restriction material ((Effigy)). This conversion prevents the gravitational potential free energy from being converted into kinetic energy of the truck. Since the mass of the truck is much greater than that of the brake material absorbing the free energy, the temperature increment may occur too fast for sufficient heat to transfer from the brakes to the surround; in other words, the brakes may overheat.
The smoking brakes on a braking truck are visible bear witness of the mechanical equivalent of rut.

Calculate the temperature increase of 10 kg of restriction material with an average specific estrus of ![]() if the material retains 10% of the energy from a 10,000-kg truck descending 75.0 m (in vertical displacement) at a constant speed.
if the material retains 10% of the energy from a 10,000-kg truck descending 75.0 m (in vertical displacement) at a constant speed.
Strategy We calculate the gravitational potential energy (Mgh) that the unabridged truck loses in its descent, equate it to the increase in the brakes' internal energy, and then observe the temperature increase produced in the restriction material alone.
Solution Kickoff nosotros calculate the change in gravitational potential energy as the truck goes downhill:
![]()
Because the kinetic free energy of the truck does not change, conservation of free energy tells the states the lost potential energy is dissipated, and we assume that 10% of it is transferred to internal energy of the brakes, so accept ![]() . So we calculate the temperature change from the heat transferred, using
. So we calculate the temperature change from the heat transferred, using
![]()
where m is the mass of the brake cloth. Insert the given values to find
![]()
Significance If the truck had been traveling for some time, then just before the descent, the restriction temperature would probably be higher than the ambient temperature. The temperature increase in the descent would likely enhance the temperature of the brake material very high, so this technique is non practical. Instead, the truck would employ the technique of engine braking. A unlike idea underlies the recent technology of hybrid and electric cars, where mechanical free energy (kinetic and gravitational potential energy) is converted by the brakes into electrical energy in the bombardment, a procedure called regenerative braking.
In a common kind of problem, objects at unlike temperatures are placed in contact with each other merely isolated from everything else, and they are allowed to come into equilibrium. A container that prevents heat transfer in or out is called a calorimeter, and the utilise of a calorimeter to make measurements (typically of rut or specific heat capacity) is called calorimetry.
We will utilise the term "calorimetry problem" to refer to any trouble in which the objects concerned are thermally isolated from their surroundings. An important idea in solving calorimetry problems is that during a heat transfer between objects isolated from their surroundings, the heat gained by the colder object must equal the heat lost by the hotter object, due to conservation of free energy:
![]()
We express this idea past writing that the sum of the heats equals nix because the estrus gained is ordinarily considered positive; the oestrus lost, negative.
Computing the Concluding Temperature in Calorimetry Suppose you pour 0.250 kg of ![]() water (about a cup) into a 0.500-kg aluminum pan off the stove with a temperature of
water (about a cup) into a 0.500-kg aluminum pan off the stove with a temperature of ![]() . Assume no heat transfer takes place to anything else: The pan is placed on an insulated pad, and heat transfer to the air is neglected in the brusque fourth dimension needed to achieve equilibrium. Thus, this is a calorimetry problem, even though no isolating container is specified. Also assume that a negligible corporeality of water boils off. What is the temperature when the water and pan reach thermal equilibrium?
. Assume no heat transfer takes place to anything else: The pan is placed on an insulated pad, and heat transfer to the air is neglected in the brusque fourth dimension needed to achieve equilibrium. Thus, this is a calorimetry problem, even though no isolating container is specified. Also assume that a negligible corporeality of water boils off. What is the temperature when the water and pan reach thermal equilibrium?
Strategy Originally, the pan and water are not in thermal equilibrium: The pan is at a higher temperature than the water. Rut transfer restores thermal equilibrium one time the water and pan are in contact; information technology stops one time thermal equilibrium betwixt the pan and the h2o is achieved. The heat lost by the pan is equal to the heat gained past the water—that is the basic principle of calorimetry.
Solution
- Utilise the equation for heat transfer
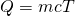 to express the heat lost by the aluminum pan in terms of the mass of the pan, the specific heat of aluminum, the initial temperature of the pan, and the final temperature:
to express the heat lost by the aluminum pan in terms of the mass of the pan, the specific heat of aluminum, the initial temperature of the pan, and the final temperature:
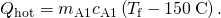
- Express the heat gained past the water in terms of the mass of the h2o, the specific heat of h2o, the initial temperature of the h2o, and the concluding temperature:
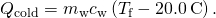
- Note that
 and
and 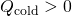 and that as stated above, they must sum to zilch:
and that as stated above, they must sum to zilch:
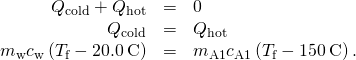
- Bring all terms involving
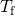 on the left hand side and all other terms on the right hand side. Solving for
on the left hand side and all other terms on the right hand side. Solving for 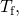
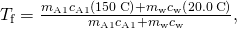
and insert the numerical values:
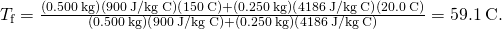
Significance Why is the final temperature and then much closer to ![]() than to
than to ![]() ? The reason is that water has a greater specific heat than about common substances and thus undergoes a smaller temperature change for a given heat transfer. A big torso of water, such equally a lake, requires a large amount of heat to increase its temperature appreciably. This explains why the temperature of a lake stays relatively abiding during the day even when the temperature change of the air is big. However, the water temperature does change over longer times (eastward.g., summer to winter).
? The reason is that water has a greater specific heat than about common substances and thus undergoes a smaller temperature change for a given heat transfer. A big torso of water, such equally a lake, requires a large amount of heat to increase its temperature appreciably. This explains why the temperature of a lake stays relatively abiding during the day even when the temperature change of the air is big. However, the water temperature does change over longer times (eastward.g., summer to winter).
Check Your Understanding If 25 kJ is necessary to raise the temperature of a rock from ![]() how much heat is necessary to oestrus the rock from
how much heat is necessary to oestrus the rock from ![]() ?
?
To a good approximation, the heat transfer depends just on the temperature deviation. Since the temperature differences are the same in both cases, the same 25 kJ is necessary in the 2nd case. (As we will run across in the next department, the respond would have been different if the object had been made of some substance that changes stage anywhere between ![]() and
and ![]() .)
.)
Temperature-Dependent Heat Capacity At low temperatures, the specific heats of solids are typically proportional to ![]() . The commencement understanding of this behavior was due to the Dutch physicist Peter Debye, who in 1912, treated atomic oscillations with the quantum theory that Max Planck had recently used for radiation. For instance, a skillful approximation for the specific heat of table salt, NaCl, is
. The commencement understanding of this behavior was due to the Dutch physicist Peter Debye, who in 1912, treated atomic oscillations with the quantum theory that Max Planck had recently used for radiation. For instance, a skillful approximation for the specific heat of table salt, NaCl, is ![]() The abiding 321 K is called the Debye temperature of NaCl,
The abiding 321 K is called the Debye temperature of NaCl, ![]() and the formula works well when
and the formula works well when ![]() Using this formula, how much heat is required to heighten the temperature of 24.0 g of NaCl from five K to 15 K?
Using this formula, how much heat is required to heighten the temperature of 24.0 g of NaCl from five K to 15 K?
Solution Because the heat capacity depends on the temperature, we need to utilise the equation
![]()
Nosotros solve this equation for Q by integrating both sides: ![]()
Then we substitute the given values in and evaluate the integral:
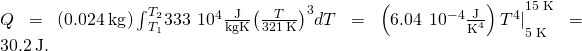
Significance If we had used the equation ![]() and the room-temperature specific heat of salt,
and the room-temperature specific heat of salt, ![]() nosotros would accept gotten a very unlike value.
nosotros would accept gotten a very unlike value.
Summary
- Oestrus and work are the 2 distinct methods of energy transfer.
- Estrus transfer to an object when its temperature changes is often approximated well by
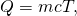 where thousand is the object's mass and c is the specific heat of the substance.
where thousand is the object's mass and c is the specific heat of the substance.
Conceptual Questions
How is heat transfer related to temperature?
Temperature differences cause heat transfer.
Describe a situation in which rut transfer occurs.
When rut transfers into a system, is the energy stored as heat? Explicate briefly.
No, information technology is stored as thermal energy. A thermodynamic system does not take a well-defined quantity of heat.
The brakes in a car increase in temperature by ![]() when bringing the car to rest from a speed v. How much greater would
when bringing the car to rest from a speed v. How much greater would ![]() be if the car initially had twice the speed? You may assume the car stops fast enough that no oestrus transfers out of the brakes.
be if the car initially had twice the speed? You may assume the car stops fast enough that no oestrus transfers out of the brakes.
Bug
On a hot day, the temperature of an 80,000-50 pond puddle increases by ![]() . What is the net heat transfer during this heating? Ignore any complications, such every bit loss of water by evaporation.
. What is the net heat transfer during this heating? Ignore any complications, such every bit loss of water by evaporation.
![]()
To sterilize a l.0-m glass baby bottle, nosotros must raise its temperature from ![]() to
to ![]() . How much heat transfer is required?
. How much heat transfer is required?
Rubbing your easily together warms them by converting work into thermal energy. If a adult female rubs her easily back and forth for a total of 20 rubs, at a altitude of 7.50 cm per rub, and with an average frictional force of 40.0 Northward, what is the temperature increment? The mass of tissues warmed is only 0.100 kg, generally in the palms and fingers.
A ![]() block of a pure material is heated from
block of a pure material is heated from ![]() to
to ![]() by the addition of 4.35 kJ of energy. Summate its specific oestrus and identify the substance of which it is most likely composed.
by the addition of 4.35 kJ of energy. Summate its specific oestrus and identify the substance of which it is most likely composed.
![]() . It is copper.
. It is copper.
Suppose identical amounts of heat transfer into different masses of copper and water, causing identical changes in temperature. What is the ratio of the mass of copper to water?
In a written report of healthy immature men1, doing 20 push-ups in ane minute burned an amount of free energy per kg that for a 70.0-kg man corresponds to 8.06 calories (kcal). How much would a 70.0-kg man'south temperature rise if he did not lose any rut during that fourth dimension?
![]()
A 1.28-kg sample of water at ![]() is in a calorimeter. Y'all drop a piece of steel with a mass of 0.385 kg at
is in a calorimeter. Y'all drop a piece of steel with a mass of 0.385 kg at ![]() into it. After the sizzling subsides, what is the last equilibrium temperature? (Brand the reasonable assumptions that any steam produced condenses into liquid water during the procedure of equilibration and that the evaporation and condensation don't affect the outcome, equally we'll see in the next section.)
into it. After the sizzling subsides, what is the last equilibrium temperature? (Brand the reasonable assumptions that any steam produced condenses into liquid water during the procedure of equilibration and that the evaporation and condensation don't affect the outcome, equally we'll see in the next section.)
Repeat the preceding problem, bold the water is in a glass beaker with a mass of 0.200 kg, which in turn is in a calorimeter. The chalice is initially at the same temperature as the h2o. Earlier doing the trouble, should the respond be higher or lower than the preceding respond? Comparison the mass and specific heat of the beaker to those of the water, do you recall the beaker will brand much difference?
It should exist lower. The chalice volition not make much difference: ![]()
Footnotes
- 1JW Vezina, "An examination of the differences between ii methods of estimating energy expenditure in resistance preparation activities," Journal of Strength and Conditioning Enquiry, April 28, 2014, http://world wide web.ncbi.nlm.nih.gov/pubmed/24402448
willinghamhishich.blogspot.com
Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/heat-transfer-specific-heat-and-calorimetry/
0 Response to "Calculate the Answer to Part B Again Using the Ideal Gas Tables Rather Than Constant Specific Heat"
Post a Comment